分布式算子开发¶
分布式算子用于在自动并行计算中自动推导输入、输出张量在设备上的切分状态,并完成对应的并行计算。由于可以自动推导输入、输出的分布情况,用户在使用自动并行时只需标记部分张量的分布情况,无需考虑每个设备内部的计算以及设备间的通信等细节,分布式算子可自动高效实现整个网络的分布式训练,大幅简化分布式程序的编写过程。
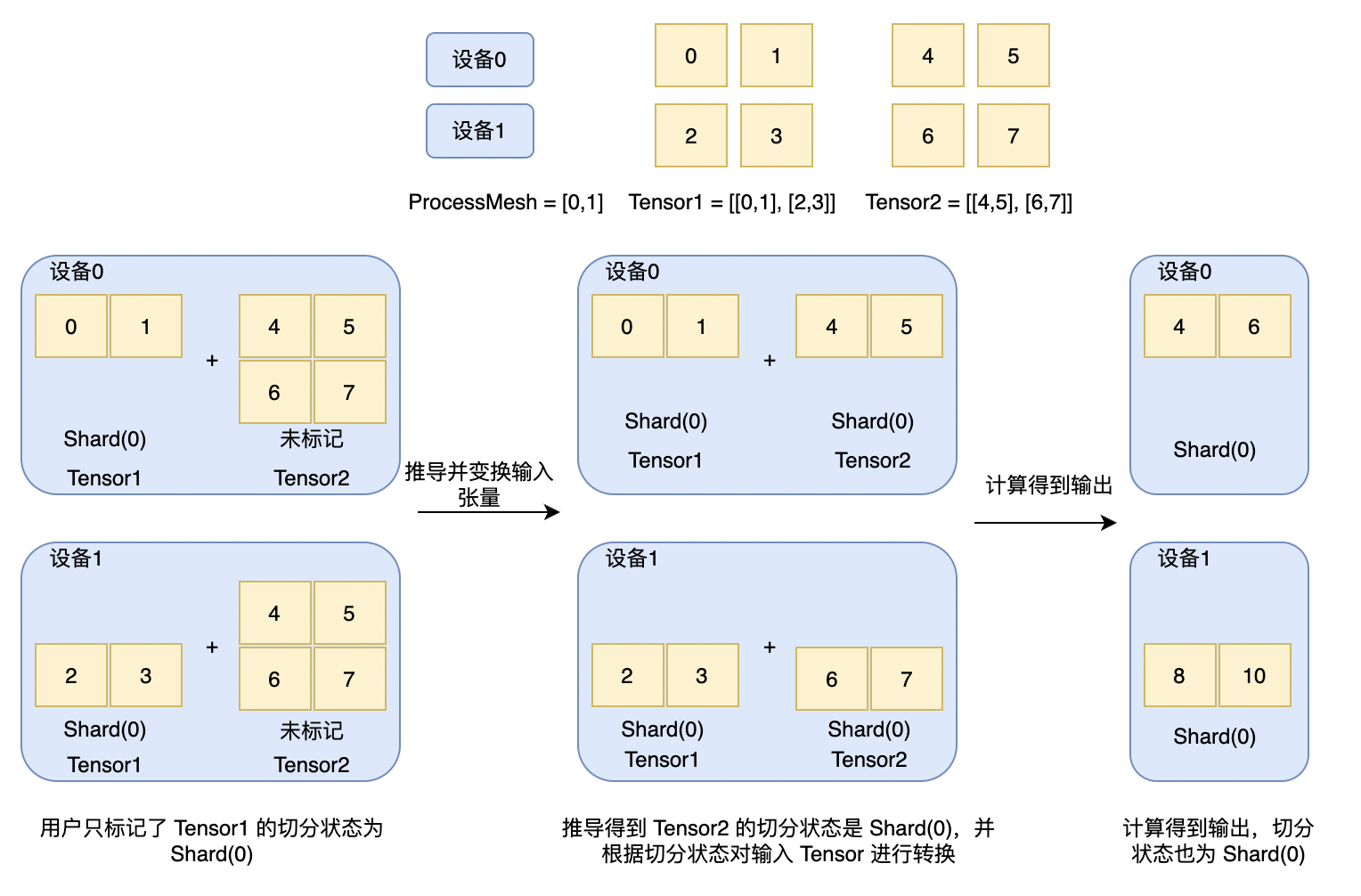
如下图所示,在执行加法计算前,用户只标记了输入 Tensor1 的切分状态为 Shard(0),因此每个设备上只有 Tensor1 的部分数据,Tensor2 没有标记,每个设备上有所有数据。在执行计算前,加法算子首先根据用户标记的张量切分状态,推导出没有标记的输入张量的切分状态,以及输出张量的切分状态,并根据推导得到的切分状态对输入张量进行转换,示例中加法算子推导出 Tensor2 和输出的切分状态为 Shard(0),并对 Tensor2 进行切分状态的转换,转换后每个设备有 Tensor2 的部分数据。 最后利用多设备进行分布式计算得到输出,示例中在每个设备上均执行加法计算,得到计算结果,其切分状态也是 Shard(0)。
飞桨已经实现了大部分常用的分布式算子,并提供一套通用机制允许用户根据需要开发自己的分布式算子。相比于单卡的算子,分布式算子仅需额外开发一个切分推导规则即可。切分推导规则主要用于推导补全模型中没有被用户标记的张量的分布情况,其决定了后续整个网络的分布式训练策略,是影响训练效率的重要模块。对于一些缺少推导规则的算子,框架提供了兜底规则,将所有输入 tensor 变换为全复制的状态进行计算,虽然效率较低,但能保证其在自动并行中正确执行。
一、基础概念¶
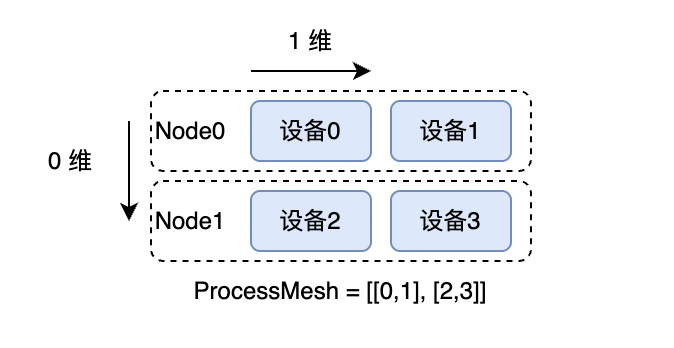
在切分推导中,我们使用 DimsMapping 来表示张量在不同设备上的分布情况。DimsMapping 和 Placements 类似,都用于表示张量在 ProcessMesh 上的分布方式,不同点在于 DimsMapping 是从张量的角度出发,描述张量每一维度的切分状态;Placements 则是从 ProcessMesh 的角度出发,描述在 ProcessMesh 的每一维度上数据的切分状态。
下图是一个 2 机 4 卡的示例,其中 ProcessMesh 被表示为 [[0, 1], [2, 3]]:
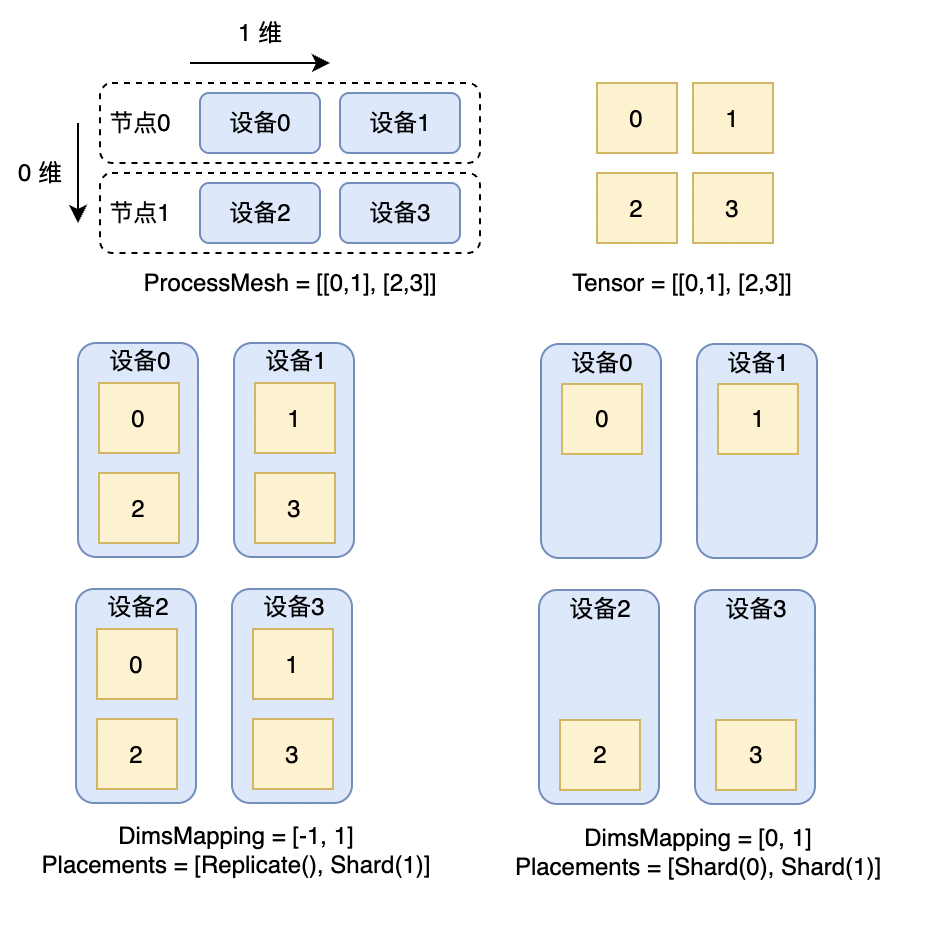
我们可以使用 DimsMapping 来表示数据在 ProcessMesh 上的分布方式,DimsMapping[i] = j 表示张量的第 i 维在 ProcessMesh 的第 j 维上被切分,若 j 为 -1 则表示不切分,在该维上复制。例如张量大小为 (4, 4),process_mesh 的大小为 [2, 2],DimsMapping = [-1, 1] 表示张量的第 0 维不切分,第 1 维在 ProcessMesh 的第 1 维上切分,切分后每个卡上的张量大小为 (2, 1),等价于 Placements 表示的 [Replicate(), Shard(1)]。DimsMapping = [0, 1] 表示张量的第 0 维在 ProcessMesh 的第 0 维上切分,第 1 维在 ProcessMesh 的第 1 维上切分,切分后每个卡上的张量大小为 (1, 1),等价于 Placements 表示的 [Shard(0), Shard(1)]。下图分别展示了 DimsMapping 为 [-1, 1] 和 [0, 1] 时的张量切分情况。
二、开发流程¶
切分推导的核心是对各张量的 DimsMapping 进行推导,由于不同类型的算子计算逻辑不同,因此其推导过程也各不相同,需要对不同类型的算子分别开发推导规则。
整体的开发过程主要包括以下步骤:
开发算子的推导规则,代码以 {op_name}.h 和 {op_name}.cc 命名(以 matmul 为例,文件名为 matmul.h 和 matmul.cc),放在 Paddle/paddle/phi/infermeta/spmd_rules 目录下。
注册规则,仿照已有规则注册新增规则,使规则在算子计算时生效。
写推导规则对应的单测,放到 Paddle/test/auto_parallel/spmd_rules 目录,写法可以参考该目录下其他单测文件,单测需要包含全面的测试用例。
2.1 接口定义¶
以加法计算为例,推导规则的接口定义如下,接口中参数需要和 phi api(Paddle/paddle/phi/api/lib/api.cc,这个文件在 cmake 之后会生成)保持一致,由于加法、减法、乘法等计算都是对两个输入张量的逐元素计算,因此可以使用同一规则,这里将规则命名为 ElementwiseBinaryInferSpmd:
namespace phi {
namespace distributed {
// add 的 phi api 为
// PADDLE_API Tensor add(const Tensor& x, const Tensor& y)
// 规则中的参数和 phi api 保持一致,如果算子 phi api 的参数包含非 tensor 的属性,规则的接口参数也需要包含,保持一致。例如:
// matmul 的 phi api 为
// PADDLE_API Tensor matmul(const Tensor& x, const Tensor& y, bool transpose_x, bool transpose_y),matmul 的推导规则接口也需要包含 transpose_x 和 transpose_y 两个输入参数
// DistMetaTensor 中包含了 tensor 的分布式属性、shape 等成员,是推导使用的主要数据结构
// 返回值的类型为 SpmdInfo,是 std::pair<std::vector<TensorDistAttr>, std::vector<TensorDistAttr>> 类型,
// 分别存储了推导得到的 op 所需要的输入分布式属性和输出 tensor 的分布式属性
SpmdInfo ElementwiseBinaryInferSpmd(const DistMetaTensor& x,
const DistMetaTensor& y)
} // namespace distributed
} // namespace phi
2.2 规则实现¶
按照算子的不同计算逻辑,规则整体上可以分为两大类,计算类和修改形状类,实现的核心思想一样,都是通过找到输入、输出维度之间的对应关系,把分布式属性在对应维度间进行传递。下面分别介绍两类推导规则的实现过程。
2.2.1 计算类规则¶
计算类规则对应于对输入进行计算的算子,例如 matmul、elementwise 等。计算类算子的推导规则基于 Einsum Notation 实现,首先找到输入张量、输出张量各维度之间的对应关系,然后把分布式属性在对应维度间进行传递。推导的具体过程如下:
根据算子的计算过程,得到对应的 Einsum Notation。Einsum Notation 反应了输入和输出之间各维度的对应关系,例如根据 matmul 的计算方式,其 Einsum Notation 为 ij, jk -> ik,表示输出 tensor 中的 (i,k) 由第一个输入的 (i,j) 和第二个输入的 (j,k) 得到,消失的维度是进行规约(这里是 j,进行求和)的维度。由此可见,Einsum Notation 中字母相同的维度就是输入、输出中对应的维度。
对输入的 DimsMapping 进行合并操作,即如果有多个输入 tensor,且 DimsMapping 不相同,计算得到一个对所有输入兼容的 DimsMapping,由此可以得到 Einsum Notation 中每个字母(维度)的 DimsMapping 值。
根据第 2 步中得到的字母(维度)和 dims mapping 值的对应关系,得到输出的 DimsMapping。
如果输入的 DimsMapping 需要更新,即算子计算时所需要的输入切分状态和输入张量当前的切分状态不同,例如第 2 步中得到的兼容值和原来的不相同、或者原来的 DimsMapping 不合法等,则进行更新。 一些基础函数已经实现在公共模块中,开发者需要根据算子计算过程构建 Einsum Notation,2、3、4 步可以调用基础函数完成。查看后文单测中的测试样例可以帮助理解推导过程。
下面以 elementwise 的推导规则为例,介绍推导规则的实现,相关说明写在注释里,相关细节可以直接看源码。
// 两个输入的 elementwise 推导规则,对应于加、减、乘、除等算子都可以用
// 这一规则进行推导
SpmdInfo ElementwiseBinaryInferSpmd(const DistMetaTensor& x,
const DistMetaTensor& y) {
// Step0: 检查输入是否合法
auto x_shape = phi::vectorize(x.dims());
int x_ndim = x_shape.size();
auto y_shape = phi::vectorize(y.dims());
int y_ndim = y_shape.size();
TensorDistAttr x_dist_attr_src = x.dist_attr();
TensorDistAttr y_dist_attr_src = y.dist_attr();
std::vector<int64_t> x_dims_mapping = x_dist_attr_src.dims_mapping();
std::vector<int64_t> y_dims_mapping = y_dist_attr_src.dims_mapping();
PADDLE_ENFORCE_EQ(x_ndim,
x_dims_mapping.size(),
phi::errors::InvalidArgument(
"ElementwiseBinary, The Tensor X's rank [%d] and X's "
"dims_mapping size [%d] are not matched.",
x_ndim,
x_dims_mapping.size()));
PADDLE_ENFORCE_EQ(y_ndim,
y_dims_mapping.size(),
phi::errors::InvalidArgument(
"ElementwiseBinary, The Tensor Y's rank [%d] and Y's "
"dims_mapping size [%d] are not matched.",
y_ndim,
y_dims_mapping.size()));
// Step1: 构建 Einsum Notation。没有广播情况下的 3 维 tensor 为例,
// elementwise 对应的 Einsum Notation 为 abc, abc --> abc
std::string x_axes, y_axes, out_axes;
GetBinaryNotations(x_shape, y_shape, &x_axes, &y_axes, &out_axes);
// Step2: Sharding Propogation
// Step2.1: 合并输入的 dims mapping,得到每一维度对应的 dims mapping 值。
// 调用 ShardingMergeForTensors 可以对输入 dims mapping 进行合并,返回的 map 即为
// 每一维度对应的 dims mapping 值。
std::unordered_map<std::string, int64_t> axis_to_dim_map =
ShardingMergeForTensors(
{{x_axes, x_dims_mapping}, {y_axes, y_dims_mapping}});
// Step2.2: Infer output dimsmapping from merged input dimsmapping
// 根据上一步得到的字母(维度)和 dims mapping 值的对应关系,得到 output 的 dims mapping。
// GetDimsMappingForAxes 可以得到所需要的 dims mapping。
std::vector<int64_t> out_dims_mapping =
GetDimsMappingForAxes(out_axes, axis_to_dim_map);
// initialize output dist_attr's process_mesh, batch_dim and dynamic dims with
// input dist_attr.
TensorDistAttr out_dist_attr = CopyTensorDistAttrForOutput(x_dist_attr_src);
// 把 output 的 dims mapping 设置为推导得到的 dims mapping
out_dist_attr.set_dims_mapping(out_dims_mapping);
// Step2.3: Update inputs' dims mapping with merged one.
TensorDistAttr x_dist_attr_dst(x_dist_attr_src);
TensorDistAttr y_dist_attr_dst(y_dist_attr_src);
// 如果合并后输入的 dims mapping 和原始的不同,同样需要更新。这里同样
// 使用 GetDimsMappingForAxes 获得输入需要更新的 dims mapping。
x_dist_attr_dst.set_dims_mapping(
GetDimsMappingForAxes(x_axes, axis_to_dim_map));
y_dist_attr_dst.set_dims_mapping(
GetDimsMappingForAxes(y_axes, axis_to_dim_map));
// Step3: Handle partial
// Handle input tensor partial (TODO)
// 打印相关信息,方便调试
VLOG(4) << "ElementwiseSPMDRule InferForward:";
VLOG(4) << "Input0 shape: [" << str_join(x_shape) << "] "
<< "src_dims_mapping: [" << str_join(x_dims_mapping) << "] "
<< "dst_dims_mapping: [" << str_join(x_dist_attr_dst.dims_mapping())
<< "]";
VLOG(4) << "Input1 shape: [" << str_join(y_shape) << "] "
<< "src_dims_mapping: [" << str_join(y_dims_mapping) << "] "
<< "dst_dims_mapping: [" << str_join(y_dist_attr_dst.dims_mapping())
<< "]";
VLOG(4) << "Output dims_mapping: [" + str_join(out_dims_mapping) + "]\n\n";
// 返回 输入、输出 的分布式属性,返回值的类型为 SpmdInfo,是
// std::pair<std::vector<TensorDistAttr>, std::vector<TensorDistAttr>> 类型
return {{x_dist_attr_dst, y_dist_attr_dst}, {out_dist_attr}};
}
注:现有代码中还有一个逆向推导规则,和前向相反,使用输出的分布式属性推导输入的分布式属性,在当前架构中逆向推导规则没有使用,可以忽略。
2.2.2 修改形状类规则¶
修改形状类规则主要指 reshape、squeeze 等修改 tensor shape 的规则,这类规则无法使用 Einsum Notation 得到输入(input)、输出(output)维度的对应关系。Paddle 中定义了 DimsTrans 的数据结构用于表示维度之间的变换,用 vector<DimsTrans*> 表示从 input shape 到 output shape 的变换,vector 的长度和 output 的 shape size 相同,表示每一维如何变换而来。DimsTrans 有 Flatten、 Split、 Singleton 和 InputDim 4 种类型,Flatten 表示该维度由 input 的若干维度合并而成;Split 表示由 input 的某一维度拆分而来;Singleton 表示这一维的大小是 1;InputDim 表示和 input 的指定维度相同。
如下图所示,对于 shape 从 input (6, 12, 24, 48) 到 output (72, 24, 6, 8),用 DimsTrans 表示为 [Flatten(InputDim(0), InputDim(1)), InputDim(2), Split(InputDim(3), (6, 8), 0), Split(InputDim(3), (6, 8), 1)]。其中第 0 个元素 Flatten(InputDim(0), InputDim(1)) 表示 output 的第 0 维由 input 的 0、1 两维合并;第 1 个元素 InputDim(2) 表示 output 的第 1 维和 input 的第 2 维相同;第 2 个元素 Split(InputDim(3), (6, 8), 0) 表示 output 的第 2 维由 input 的第 3 维拆分而来,拆分的形状是 (6,8),output 的第 2 维是拆分后的第一个维度;第 3 个元素 Split(InputDim(3), (6, 8), 1)同理,表示 output 的第 3 维是拆分后的第 1 个维度。
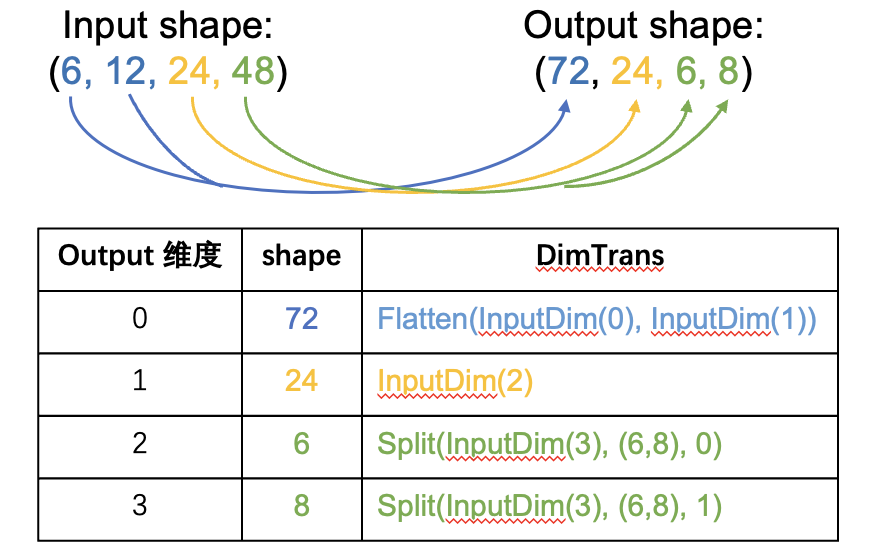
(6, 12, 24, 48) --> (72, 24, 6, 8) 的变换关系
修改形状类推导规则的具体过程如下:
根据 input 和 output 的 shape,计算得到从 input 到 output 的变换关系。
根据第 1 步求得的变换关系推导 output 的 dims mapping。
更新 input (如果需要) 和 output 的 dims mapping 同样的,一些基础函数已经实现在公共函数里,开发者需要根据 op 的特征构建 input、output 之间的变换关系,然后调用基础函数推导得到 dims mapping。
下面以 reshape 为例,介绍推导规则的实现,相关说明写在注释里,相关细节可以直接看源码。
SpmdInfo ReshapeInferSpmd(const DistMetaTensor& x,
const std::vector<int64_t>& shape) {
// Step0: 检查输入是否合法
auto src_shape = phi::vectorize(x.dims());
int x_ndim = src_shape.size();
auto x_dist_attr_src = x.dist_attr();
std::vector<int64_t> x_dims_mapping = x_dist_attr_src.dims_mapping();
PADDLE_ENFORCE_EQ(
x_ndim,
x_dims_mapping.size(),
phi::errors::InvalidArgument("The Tensor X's rank [%d] and X's "
"dims_mapping size [%d] are not matched.",
x_ndim,
x_dims_mapping.size()));
// Step1: 根据 input 和 output 的 shape,构建从输入到输出的变换关系
// handle the '0' values in target shape, '0' indicates
// that the target shape is equal to the source shape
std::vector<int64_t> tgt_shape(shape);
for (int64_t i = 0, n = static_cast<int64_t>(tgt_shape.size()); i < n; i++) {
if (tgt_shape[i] == 0) {
tgt_shape[i] = src_shape[i];
}
}
// MakeReshapeDimTrans 用于构建 reshape 的变换关系,对于其他 op,开发者需要
// 实现对应的方法。该函数会返回一个 DimTrans 的 vector,表示从 src_shape 到
// tgt_shape 的变换。
std::vector<DimTrans*> trans = MakeReshapeDimTrans(src_shape, tgt_shape);
// Step2: 由 Step1 的到的 std::vector<DimTrans*>,调用 InferFromDimTrans
// 就可以得到 output 的 dims_mapping。返回值中,dims_mapping_vec[0] 是 input
// 的 dims mapping,dims_mapping_vec[1] 是 output 的 dims mapping。
std::vector<std::vector<int64_t>> dims_mapping_vec =
InferFromDimTrans(x, trans);
// Step3: 更新 input、output 的 dims_mapping。
TensorDistAttr x_dist_attr_dst(x_dist_attr_src);
x_dist_attr_dst.set_dims_mapping(dims_mapping_vec[0]);
TensorDistAttr out_dist_attr(x_dist_attr_src);
out_dist_attr.set_dims_mapping(dims_mapping_vec[1]);
VLOG(4) << "ReshapeInferSpmd: X shape: [" << str_join(src_shape)
<< "] Out shape: [" << str_join(tgt_shape) << "]";
VLOG(4) << "Transformation from input to output:";
for (int64_t i = 0, n = static_cast<int64_t>(trans.size()); i < n; i++) {
DimTrans* t = trans[i];
VLOG(4) << "\tOut axis[" << i << "]: " << t->to_string();
}
VLOG(4) << "X dims_mapping_src: [" << str_join(x_dims_mapping)
<< "] dims_mapping_dst: [" << str_join(dims_mapping_vec[0])
<< "]\n Out dims_mapping: [" << str_join(dims_mapping_vec[1])
<< "]\n\n";
// 清理 vector<DimTrans*>
CleanUp();
return {{x_dist_attr_dst}, {out_dist_attr}};
}
2.3 规则注册¶
规则实现后需要在 yaml 文件中 op 的配置里加上该 op 所使用的切分推导规则,使该规则生效,如果 op 没有切分推导规则,则该 op 在计算时会使用全复制的兜底规则,把所有的输入张量都转换为全复制状态进行计算,效率较低。下面的代码展示了如何注册规则,只需要在配置 op 的 yaml 文件里加上 spmd_rule 字段即可,spmd_rule 的值是切分推导规则的函数名。
此外,这种直接配置的方式也可方便用户直接复用现有的规则,如果某个 op 没有在 yaml 中添加推导规则,但该 op 所需要的规则已经在框架中实现了,则直接在 yaml 文件里添加即可。
- op : relu
args : (Tensor x)
output : Tensor(out)
infer_meta :
func : UnchangedInferMeta
spmd_rule : ElementwiseUnaryInferSpmd # 在 infer_meta 字段里新增 spmd_rule,通过函数名指定所使用的规则
kernel :
func : relu
inplace : (x -> out)
backward : relu_grad
interfaces : paddle::dialect::InferSymbolicShapeInterface
规则实现后需要在 Paddle/paddle/phi/infermeta/spmd_rules/rules.h 里添加对应规则的头文件,其他文件只需使用该头文件即可使用所有推导规则,例如在 rules.h 里添加 elementwise 规则的头文件,其中包含了 elementwise 规则的声明:
#pragma once
#include "paddle/phi/core/distributed/auto_parallel/inferspmd_utils.h"
...
#include "paddle/phi/infermeta/spmd_rules/elementwise.h"
为方便后续写单测时直接从 python 端获取该规则,可在 Paddle/paddle/phi/infermeta/spmd_rules/rules.cc 文件里注册规则。elementwise 的注册如下:
PD_REGISTER_SPMD_RULE(
elementwise_unary, // 在 python 端使用该名称获取规则
PD_INFER_SPMD(phi::distributed::ElementwiseUnaryInferSpmd),
PD_INFER_SPMD(phi::distributed::ElementwiseUnaryInferSpmdReverse));
2.4 单测¶
推导规则的单测使用 python 中的 unittest 进行开发,放到 Paddle/test/auto_parallel/spmd_rules 目录下,命名为 test_{op_name}_rule.py。在安装了新编译的 paddle python 包后,直接 python 运行单测文件进行测试。可以仿照现有的单测写,elementwise 的单测代码如下。
class TestElementwiseSPMDRule(unittest.TestCase):
def setUp(self):
# 获取规则
self.unary_rule = core.get_phi_spmd_rule("elementwise_unary") # 使用上文 rules.cc 注册规则时的名字获取规则
self.binary_rule = core.get_phi_spmd_rule("add")
x_shape = [64, 36]
y_shape = [64, 36]
process_mesh = auto.ProcessMesh(mesh=[0, 1, 2, 3])
# 定义数据结构,目前 python 端使用 DistTensorSpec 这个数据结构作为输入
x_tensor_dist_attr = TensorDistAttr()
x_tensor_dist_attr.dims_mapping = [1, 0]
x_tensor_dist_attr.process_mesh = process_mesh
self.x_dist_tensor_spec = DistTensorSpec(x_shape, x_tensor_dist_attr)
y_tensor_dist_attr = TensorDistAttr()
y_tensor_dist_attr.dims_mapping = [0, -1]
y_tensor_dist_attr.process_mesh = process_mesh
self.y_dist_tensor_spec = DistTensorSpec(y_shape, y_tensor_dist_attr)
self.out_dist_tensor_spec = DistTensorSpec(self.x_dist_tensor_spec)
self.attrs = []
# 正向推导单测
def test_single_mesh_dim(self):
# [0, -1], [-1, -1] --> [0, -1], [0, -1], [0, -1]
# 设置输入的 dims mapping
self.x_dist_tensor_spec.set_dims_mapping([0, -1])
self.y_dist_tensor_spec.set_dims_mapping([-1, -1])
# 调用规则进行推导,如果规则有其他属性,比如 matmul 有 trans_x, trans_y,
# 直接放到 spec 的后面
result_dist_attrs = self.binary_rule.infer_forward(
self.x_dist_tensor_spec, self.y_dist_tensor_spec
)
infered_input_dist_attrs = result_dist_attrs[0] # 推导得到的 input dims mapping
infered_output_dist_attrs = result_dist_attrs[1] # 推导得到的 output dims mapping
# 检查结果是否正确
self.assertEqual(infered_input_dist_attrs[0].dims_mapping, [0, -1])
self.assertEqual(infered_input_dist_attrs[1].dims_mapping, [0, -1])
self.assertEqual(infered_output_dist_attrs[0].dims_mapping, [0, -1])
# 逆向推导单测
def test_backward_multi_mesh_dim(self):
process_mesh = auto.ProcessMesh([[0, 1, 2], [3, 4, 5]])
self.x_dist_tensor_spec.set_process_mesh(process_mesh)
self.y_dist_tensor_spec.set_process_mesh(process_mesh)
self.x_dist_tensor_spec.shape = [96, 24, 48]
self.y_dist_tensor_spec.shape = [96, 24, 48]
self.out_dist_tensor_spec.shape = [96, 24, 48]
# [0, 1, -1] --> [0, 1, -1], [0, 1, -1], [0, 1, -1] (output --> inputs, output)
self.out_dist_tensor_spec.set_dims_mapping([0, 1, -1])
# 逆向推导把输入和输出一起作为规则的参数
resulted_dist_attrs = self.binary_rule.infer_backward(
self.x_dist_tensor_spec,
self.y_dist_tensor_spec,
self.out_dist_tensor_spec,
)
infered_input_dist_attrs = resulted_dist_attrs[0]
infered_output_dist_attrs = resulted_dist_attrs[1]
self.assertEqual(len(resulted_dist_attrs), 2)
self.assertEqual(len(infered_input_dist_attrs), 2)
self.assertEqual(len(infered_output_dist_attrs), 1)
self.assertEqual(infered_input_dist_attrs[0].dims_mapping, [0, 1, -1])
self.assertEqual(infered_input_dist_attrs[1].dims_mapping, [0, 1, -1])
self.assertEqual(infered_output_dist_attrs[0].dims_mapping, [0, 1, -1])
三、自定义算子¶
自定义算子允许用户在不修改 paddle 源代码的情况下,新增 op,扩展框架的能力。在自动并行中使用自定义算子时,也需要实现对应的切分推导规则,否则框架将使用默认的兜底规则,将所有输入 tensor 变换为全复制的状态进行计算,效率较低。
自定义算子切分推导规则的开发方式和其他算子相同,可参考前文进行开发。完成开发后,在使用 PD_BUILD_OP 构建自定义算子时添加对应的切分推导规则即可。下面代码展示了如何在构建 custom_concat_with_attr 自定义算子时添加对应的切分推导规则,首先需要额外 引入头文件 paddle/phi/api/ext/spmd_infer.h,使用用宏 CUSTOM_OP_WITH_SPMD 可以前向兼容没有规则的代码;然后在 PD_BUILD_OP (构建反向 op 使用 PD_BUILD_GRAD_OP)中添加 .SetInferSpmdRule(PD_INFER_SPMD_RULE(custom_rule)) 即可,其中 custom_rule 为新增规则的函数名。
#ifdef CUSTOM_OP_WITH_SPMD
#include "paddle/phi/api/ext/spmd_infer.h"
#endif
PD_BUILD_OP(custom_concat_with_attr)
.Inputs({paddle::Vec("X")})
.Outputs({"Out"})
.Attrs({"axis: int64_t"})
.SetKernelFn(PD_KERNEL(ConcatForwardStaticAxis))
.SetInferShapeFn(PD_INFER_SHAPE(ConcatInferShapeStaticAxis))
.SetInferDtypeFn(PD_INFER_DTYPE(ConcatInferDtypeStaticAxis))
#ifdef CUSTOM_OP_WITH_SPMD
.SetInferSpmdRule(PD_INFER_SPMD_RULE(custom_rule)) // custom_rule 为自定义规则的函数名
#endif
;
PD_BUILD_GRAD_OP(custom_concat_with_attr)
.Inputs({paddle::Vec("X"), paddle::Grad("Out")})
.Outputs({paddle::Grad(paddle::Vec("X"))})
.Attrs({"axis: int64_t"})
.SetKernelFn(PD_KERNEL(ConcatBackwardStaticAxis))
#ifdef CUSTOM_OP_WITH_SPMD
.SetInferSpmdRule(PD_INFER_SPMD_RULE(custom_grad_rule)) // custom_grad_rule 为自定义规则的函数
#endif
;
此外,自定义算子也可以复用现有的切分推导规则,例如自定义的 relu 算子,如果只改变了实现方式,算子的行为和原来的 relu 算子相同,则直接复用 ElementwiseUnary 规则(ElementwiseUnaryInferSpmd)即可,在复用时需要包含 Paddle/paddle/phi/infermeta/spmd_rules/rules.h 头文件:
#ifdef CUSTOM_OP_WITH_SPMD
#include "paddle/phi/infermeta/spmd_rules/rules.h"
#include "paddle/phi/api/ext/spmd_infer.h"
#endif
PD_BUILD_OP(custom_relu)
.Inputs({"X"})
.Outputs({"Out"})
.SetKernelFn(PD_KERNEL(ReluCUDAForward))
#ifdef CUSTOM_OP_WITH_SPMD
.SetInferSpmdRule(PD_INFER_SPMD_RULE(ElementwiseUnary))
#endif
;
注:关于构建自定义算子的更多细节,请参考自定义 C++算子。