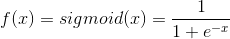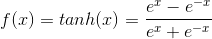数字识别¶
本教程源代码目录在book/recognize_digits,初次使用请您参考Book文档使用说明。
说明:¶
- 硬件环境要求: 本文可支持在CPU、GPU下运行
- Docker镜像支持的CUDA/cuDNN版本: 如果使用了Docker运行Book,请注意:这里所提供的默认镜像的GPU环境为 CUDA 8/cuDNN 5,对于NVIDIA Tesla V100等要求CUDA 9的 GPU,使用该镜像可能会运行失败。
- 文档和脚本中代码的一致性问题: 请注意:为使本文更加易读易用,我们拆分、调整了train.py的代码并放入本文。本文中代码与train.py的运行结果一致,可直接运行train.py进行验证。
背景介绍¶
当我们学习编程的时候,编写的第一个程序一般是实现打印"Hello World"。而机器学习(或深度学习)的入门教程,一般都是 MNIST 数据库上的手写识别问题。原因是手写识别属于典型的图像分类问题,比较简单,同时MNIST数据集也很完备。MNIST数据集作为一个简单的计算机视觉数据集,包含一系列如图1所示的手写数字图片和对应的标签。图片是28x28的像素矩阵,标签则对应着0~9的10个数字。每张图片都经过了大小归一化和居中处理。
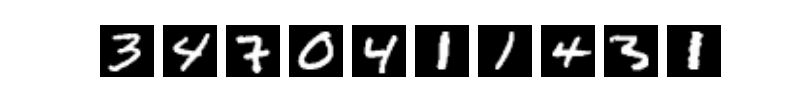
图1. MNIST图片示例
MNIST数据集是从 NIST 的Special Database 3(SD-3)和Special Database 1(SD-1)构建而来。由于SD-3是由美国人口调查局的员工进行标注,SD-1是由美国高中生进行标注,因此SD-3比SD-1更干净也更容易识别。Yann LeCun等人从SD-1和SD-3中各取一半作为MNIST的训练集(60000条数据)和测试集(10000条数据),其中训练集来自250位不同的标注员,此外还保证了训练集和测试集的标注员是不完全相同的。
MNIST吸引了大量的科学家基于此数据集训练模型,1998年,LeCun分别用单层线性分类器、多层感知器(Multilayer Perceptron, MLP)和多层卷积神经网络LeNet进行实验,使得测试集上的误差不断下降(从12%下降到0.7%)[1]。在研究过程中,LeCun提出了卷积神经网络(Convolutional Neural Network),大幅度地提高了手写字符的识别能力,也因此成为了深度学习领域的奠基人之一。此后,科学家们又基于K近邻(K-Nearest Neighbors)算法[2]、支持向量机(SVM)[3]、神经网络[4-7]和Boosting方法[8]等做了大量实验,并采用多种预处理方法(如去除歪曲、去噪、模糊等)来提高识别的准确率。
如今的深度学习领域,卷积神经网络占据了至关重要的地位,从最早Yann LeCun提出的简单LeNet,到如今ImageNet大赛上的优胜模型VGGNet、GoogLeNet、ResNet等(请参见图像分类 教程),人们在图像分类领域,利用卷积神经网络得到了一系列惊人的结果。
本教程中,我们从简单的Softmax回归模型开始,带大家了解手写字符识别,并向大家介绍如何改进模型,利用多层感知机(MLP)和卷积神经网络(CNN)优化识别效果。
模型概览¶
基于MNIST数据集训练一个分类器,在介绍本教程使用的三个基本图像分类网络前,我们先给出一些定义:
- $X$是输入:MNIST图片是$28\times28$ 的二维图像,为了进行计算,我们将其转化为$784$维向量,即$X=\left ( x_0, x_1, \dots, x_{783} \right )$。
- $Y$是输出:分类器的输出是10类数字(0-9),即$Y=\left ( y_0, y_1, \dots, y_9 \right )$,每一维$y_i$代表图片分类为第$i$类数字的概率。
- $Label$是图片的真实标签:$Label=\left ( l_0, l_1, \dots, l_9 \right )$也是10维,但只有一维为1,其他都为0。例如某张图片上的数字为2,则它的标签为$(0,0,1,0, \dot, 0)$
Softmax回归(Softmax Regression)¶
最简单的Softmax回归模型是先将输入层经过一个全连接层得到特征,然后直接通过 softmax 函数计算多个类别的概率并输出[9]。
输入层的数据$X$传到输出层,在激活操作之前,会乘以相应的权重 $W$ ,并加上偏置变量 $b$ ,具体如下:
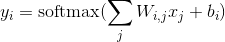
其中
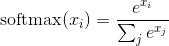
图2为softmax回归的网络图,图中权重用蓝线表示、偏置用红线表示、+1代表偏置参数的系数为1。
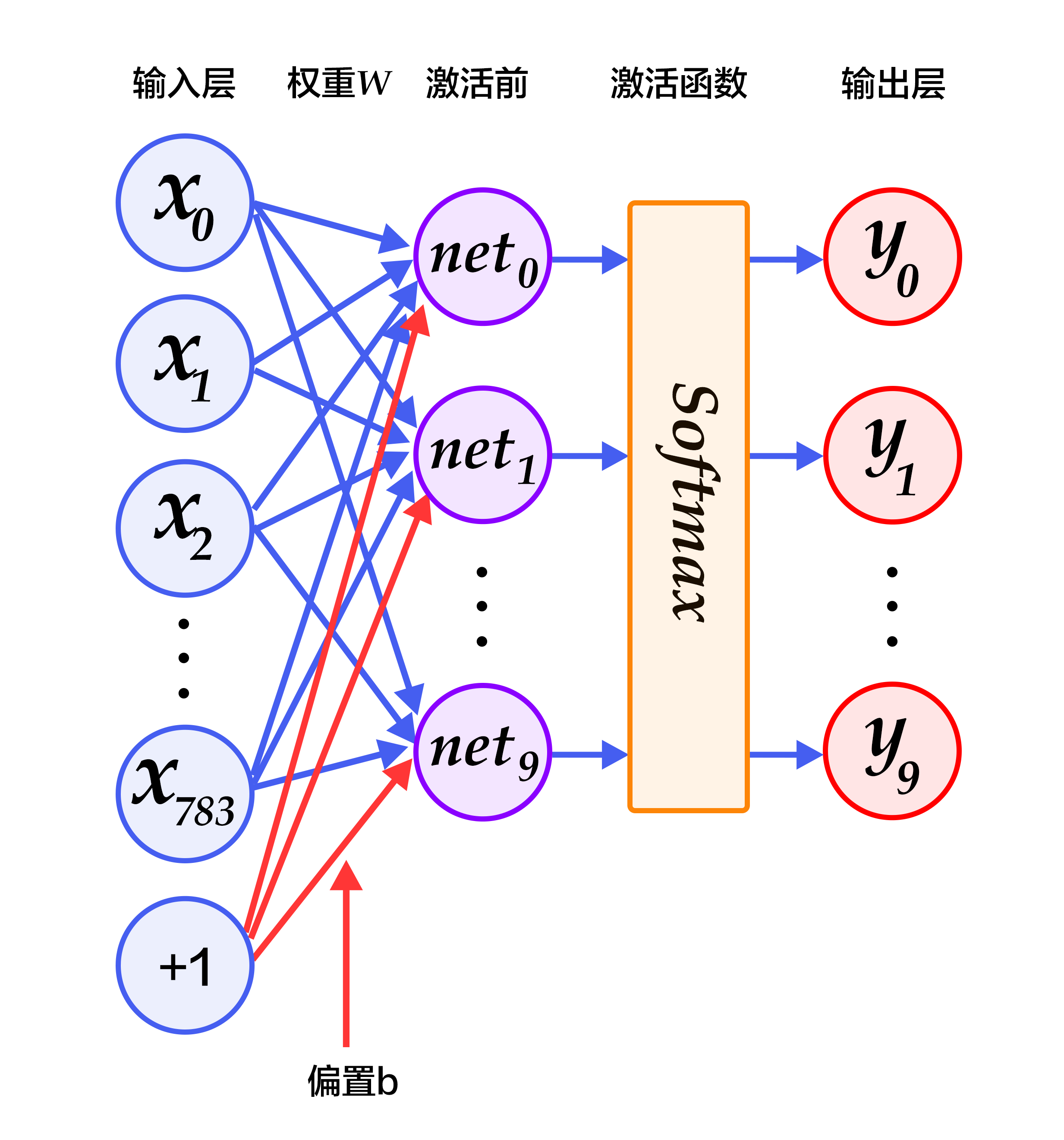
图2. softmax回归网络结构图
对于有 $N$ 个类别的多分类问题,指定 $N$ 个输出节点,$N$ 维结果向量经过softmax将归一化为 $N$ 个[0,1]范围内的实数值,分别表示该样本属于这 $N$ 个类别的概率。此处的 $y_i$ 即对应该图片为数字 $i$ 的预测概率。
在分类问题中,我们一般采用交叉熵代价损失函数(cross entropy loss),公式如下:
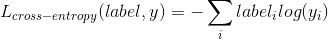
多层感知机(Multilayer Perceptron, MLP)¶
Softmax回归模型采用了最简单的两层神经网络,即只有输入层和输出层,因此其拟合能力有限。为了达到更好的识别效果,我们考虑在输入层和输出层中间加上若干个隐藏层[10]。
- 经过第一个隐藏层,可以得到 $ H_1 = \phi(W_1X + b_1) $,其中$\phi$代表激活函数,常见的有sigmoid、tanh或ReLU等函数。
- 经过第二个隐藏层,可以得到 $ H_2 = \phi(W_2H_1 + b_2) $。
- 最后,再经过输出层,得到的$Y=\text{softmax}(W_3H_2 + b_3)$,即为最后的分类结果向量。
图3为多层感知器的网络结构图,图中权重用蓝线表示、偏置用红线表示、+1代表偏置参数的系数为1。
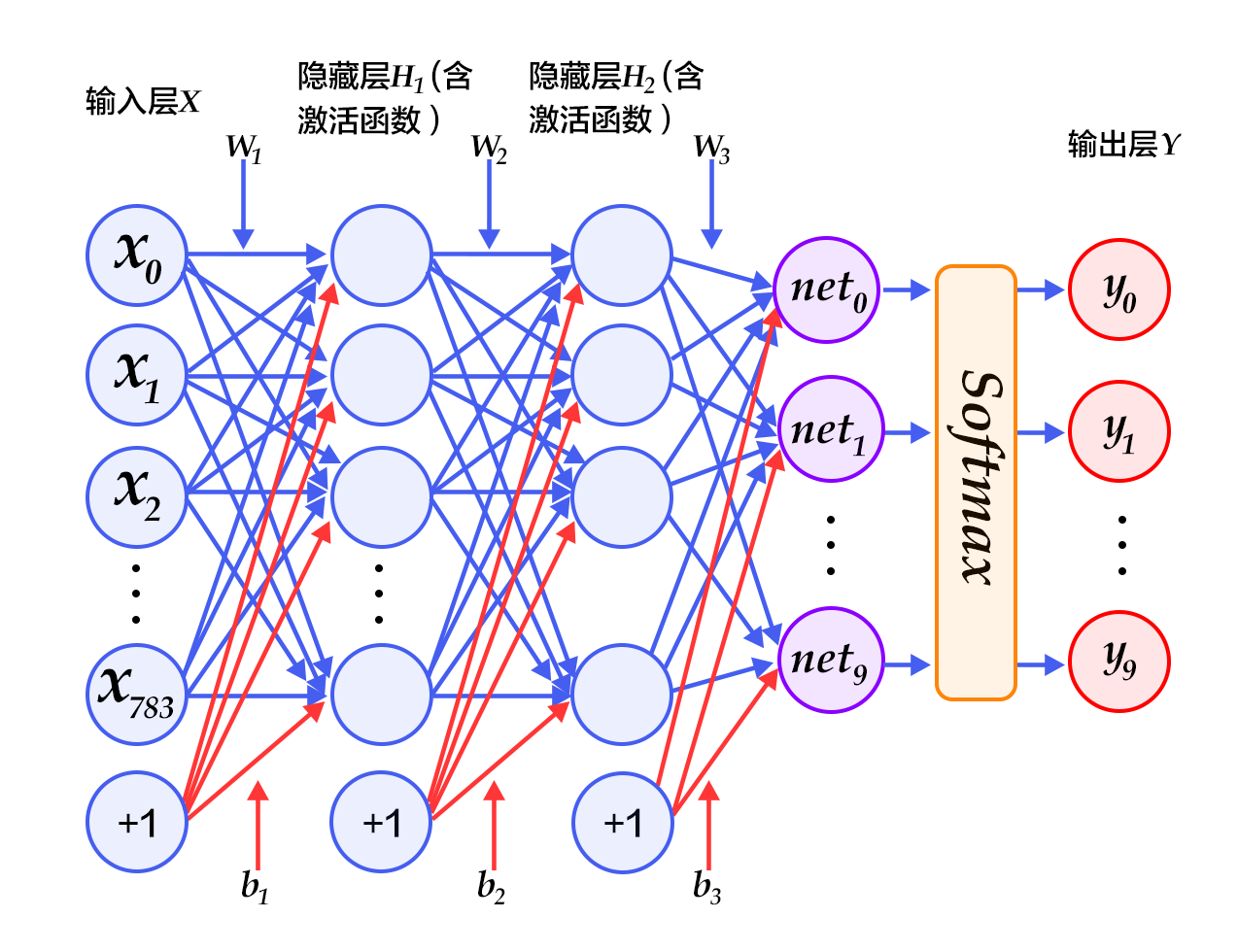
图3. 多层感知器网络结构图
卷积神经网络(Convolutional Neural Network, CNN)¶
在多层感知器模型中,将图像展开成一维向量输入到网络中,忽略了图像的位置和结构信息,而卷积神经网络能够更好的利用图像的结构信息。LeNet-5是一个较简单的卷积神经网络。图4显示了其结构:输入的二维图像,先经过两次卷积层到池化层,再经过全连接层,最后使用softmax分类作为输出层。下面我们主要介绍卷积层和池化层。
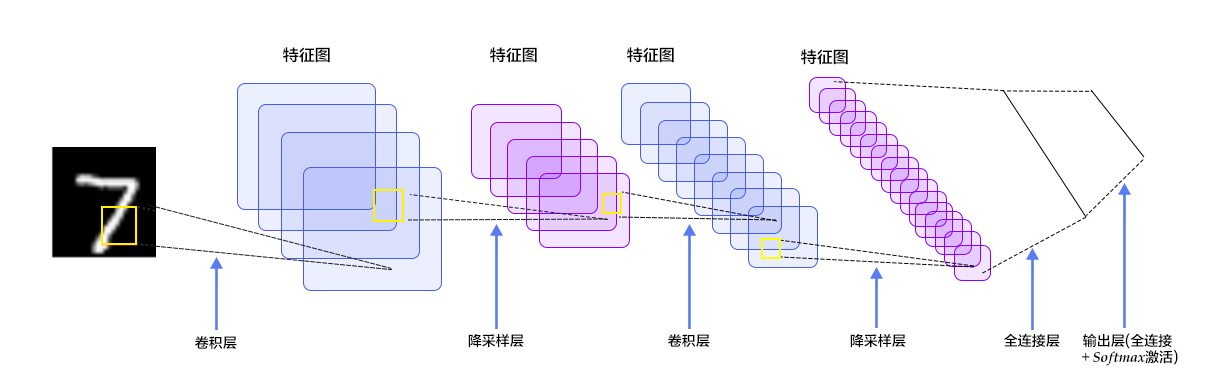
图4. LeNet-5卷积神经网络结构
卷积层¶
卷积层是卷积神经网络的核心基石。在图像识别里我们提到的卷积是二维卷积,即离散二维滤波器(也称作卷积核)与二维图像做卷积操作,简单的讲是二维滤波器滑动到二维图像上所有位置,并在每个位置上与该像素点及其领域像素点做内积。卷积操作被广泛应用与图像处理领域,不同卷积核可以提取不同的特征,例如边沿、线性、角等特征。在深层卷积神经网络中,通过卷积操作可以提取出图像低级到复杂的特征。
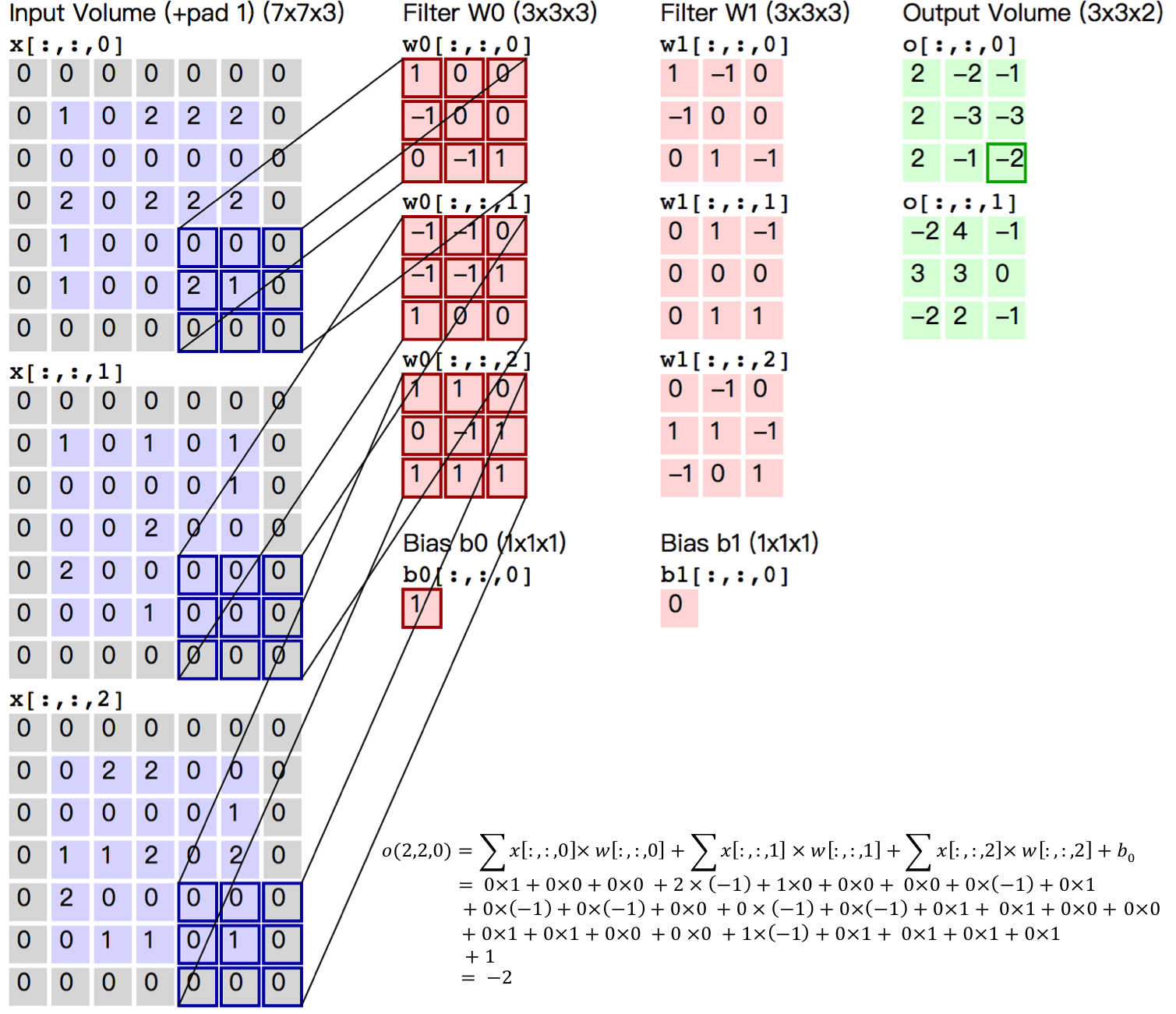
图5. 卷积层图片
图5给出一个卷积计算过程的示例图,输入图像大小为$H=5,W=5,D=3$,即$5 \times 5$大小的3通道(RGB,也称作深度)彩色图像。
这个示例图中包含两(用$K$表示)组卷积核,即图中$Filter W_0$ 和 $Filter W_1$。在卷积计算中,通常对不同的输入通道采用不同的卷积核,如图示例中每组卷积核包含($D=3)$个$3 \times 3$(用$F \times F$表示)大小的卷积核。另外,这个示例中卷积核在图像的水平方向($W$方向)和垂直方向($H$方向)的滑动步长为2(用$S$表示);对输入图像周围各填充1(用$P$表示)个0,即图中输入层原始数据为蓝色部分,灰色部分是进行了大小为1的扩展,用0来进行扩展。经过卷积操作得到输出为$3 \times 3 \times 2$(用$H_{o} \times W_{o} \times K$表示)大小的特征图,即$3 \times 3$大小的2通道特征图,其中$H_o$计算公式为:$H_o = (H - F + 2 \times P)/S + 1$,$W_o$同理。 而输出特征图中的每个像素,是每组滤波器与输入图像每个特征图的内积再求和,再加上偏置$b_o$,偏置通常对于每个输出特征图是共享的。输出特征图$o[:,:,0]$中的最后一个$-2$计算如图5右下角公式所示。
在卷积操作中卷积核是可学习的参数,经过上面示例介绍,每层卷积的参数大小为$D \times F \times F \times K$。在多层感知器模型中,神经元通常是全部连接,参数较多。而卷积层的参数较少,这也是由卷积层的主要特性即局部连接和共享权重所决定。
- 局部连接:每个神经元仅与输入神经元的一块区域连接,这块局部区域称作感受野(receptive field)。在图像卷积操作中,即神经元在空间维度(spatial dimension,即上图示例H和W所在的平面)是局部连接,但在深度上是全部连接。对于二维图像本身而言,也是局部像素关联较强。这种局部连接保证了学习后的过滤器能够对于局部的输入特征有最强的响应。局部连接的思想,也是受启发于生物学里面的视觉系统结构,视觉皮层的神经元就是局部接受信息的。
- 权重共享:计算同一个深度切片的神经元时采用的滤波器是共享的。例如图4中计算$o[:,:,0]$的每个每个神经元的滤波器均相同,都为$W_0$,这样可以很大程度上减少参数。共享权重在一定程度上讲是有意义的,例如图片的底层边缘特征与特征在图中的具体位置无关。但是在一些场景中是无意的,比如输入的图片是人脸,眼睛和头发位于不同的位置,希望在不同的位置学到不同的特征 (参考斯坦福大学公开课)。请注意权重只是对于同一深度切片的神经元是共享的,在卷积层,通常采用多组卷积核提取不同特征,即对应不同深度切片的特征,不同深度切片的神经元权重是不共享。另外,偏重对同一深度切片的所有神经元都是共享的。
通过介绍卷积计算过程及其特性,可以看出卷积是线性操作,并具有平移不变性(shift-invariant),平移不变性即在图像每个位置执行相同的操作。卷积层的局部连接和权重共享使得需要学习的参数大大减小,这样也有利于训练较大卷积神经网络。
关于卷积的更多内容可参考阅读。
数据介绍¶
PaddlePaddle在API中提供了自动加载MNIST数据的模块paddle.dataset.mnist。加载后的数据位于/home/username/.cache/paddle/dataset/mnist下:
| 文件名称 | 说明 |
|---|---|
| train-images-idx3-ubyte | 训练数据图片,60,000条数据 |
| train-labels-idx1-ubyte | 训练数据标签,60,000条数据 |
| t10k-images-idx3-ubyte | 测试数据图片,10,000条数据 |
| t10k-labels-idx1-ubyte | 测试数据标签,10,000条数据 |
Fluid API 概述¶
演示将使用最新的 Fluid API。Fluid API是最新的 PaddlePaddle API。它在不牺牲性能的情况下简化了模型配置。 我们建议使用 Fluid API,它易学易用的特性将帮助您快速完成机器学习任务。。
下面是 Fluid API 中几个重要概念的概述:
inference_program:指定如何从数据输入中获得预测的函数, 这是指定网络流的地方。train_program:指定如何从inference_program和标签值中获取loss的函数, 这是指定损失计算的地方。optimizer_func: 指定优化器配置的函数,优化器负责减少损失并驱动训练,Paddle 支持多种不同的优化器。
在下面的代码示例中,我们将深入了解它们。
配置说明¶
加载 PaddlePaddle 的 Fluid API 包。
from __future__ import print_function # 将python3中的print特性导入当前版本
import os
from PIL import Image # 导入图像处理模块
import matplotlib.pyplot as plt
import numpy
import paddle # 导入paddle模块
import paddle.fluid as fluid
Program Functions 配置¶
我们需要设置 inference_program 函数。我们想用这个程序来演示三个不同的分类器,每个分类器都定义为 Python 函数。
我们需要将图像数据输入到分类器中。Paddle 为读取数据提供了一个特殊的层 layer.data 层。
让我们创建一个数据层来读取图像并将其连接到分类网络。
- Softmax回归:只通过一层简单的以softmax为激活函数的全连接层,就可以得到分类的结果。
def softmax_regression():
"""
定义softmax分类器:
一个以softmax为激活函数的全连接层
Return:
predict_image -- 分类的结果
"""
# 输入的原始图像数据,大小为28*28*1
img = fluid.layers.data(name='img', shape=[1, 28, 28], dtype='float32')
# 以softmax为激活函数的全连接层,输出层的大小必须为数字的个数10
predict = fluid.layers.fc(
input=img, size=10, act='softmax')
return predict
- 多层感知器:下面代码实现了一个含有两个隐藏层(即全连接层)的多层感知器。其中两个隐藏层的激活函数均采用ReLU,输出层的激活函数用Softmax。
def multilayer_perceptron():
"""
定义多层感知机分类器:
含有两个隐藏层(全连接层)的多层感知器
其中前两个隐藏层的激活函数采用 ReLU,输出层的激活函数用 Softmax
Return:
predict_image -- 分类的结果
"""
# 输入的原始图像数据,大小为28*28*1
img = fluid.layers.data(name='img', shape=[1, 28, 28], dtype='float32')
# 第一个全连接层,激活函数为ReLU
hidden = fluid.layers.fc(input=img, size=200, act='relu')
# 第二个全连接层,激活函数为ReLU
hidden = fluid.layers.fc(input=hidden, size=200, act='relu')
# 以softmax为激活函数的全连接输出层,输出层的大小必须为数字的个数10
prediction = fluid.layers.fc(input=hidden, size=10, act='softmax')
return prediction
- 卷积神经网络LeNet-5: 输入的二维图像,首先经过两次卷积层到池化层,再经过全连接层,最后使用以softmax为激活函数的全连接层作为输出层。
def convolutional_neural_network():
"""
定义卷积神经网络分类器:
输入的二维图像,经过两个卷积-池化层,使用以softmax为激活函数的全连接层作为输出层
Return:
predict -- 分类的结果
"""
# 输入的原始图像数据,大小为28*28*1
img = fluid.layers.data(name='img', shape=[1, 28, 28], dtype='float32')
# 第一个卷积-池化层
# 使用20个5*5的滤波器,池化大小为2,池化步长为2,激活函数为Relu
conv_pool_1 = fluid.nets.simple_img_conv_pool(
input=img,
filter_size=5,
num_filters=20,
pool_size=2,
pool_stride=2,
act="relu")
conv_pool_1 = fluid.layers.batch_norm(conv_pool_1)
# 第二个卷积-池化层
# 使用50个5*5的滤波器,池化大小为2,池化步长为2,激活函数为Relu
conv_pool_2 = fluid.nets.simple_img_conv_pool(
input=conv_pool_1,
filter_size=5,
num_filters=50,
pool_size=2,
pool_stride=2,
act="relu")
# 以softmax为激活函数的全连接输出层,输出层的大小必须为数字的个数10
prediction = fluid.layers.fc(input=conv_pool_2, size=10, act='softmax')
return prediction
Train Program 配置¶
然后我们需要设置训练程序 train_program。它首先从分类器中进行预测。
在训练期间,它将从预测中计算 avg_cost。
注意: 训练程序应该返回一个数组,第一个返回参数必须是 avg_cost。训练器使用它来计算梯度。
请随意修改代码,测试 Softmax 回归 softmax_regression, MLP 和 卷积神经网络 convolutional neural network 分类器之间的不同结果。
def train_program():
"""
配置train_program
Return:
predict -- 分类的结果
avg_cost -- 平均损失
acc -- 分类的准确率
"""
# 标签层,名称为label,对应输入图片的类别标签
label = fluid.layers.data(name='label', shape=[1], dtype='int64')
# predict = softmax_regression() # 取消注释将使用 Softmax回归
# predict = multilayer_perceptron() # 取消注释将使用 多层感知器
predict = convolutional_neural_network() # 取消注释将使用 LeNet5卷积神经网络
# 使用类交叉熵函数计算predict和label之间的损失函数
cost = fluid.layers.cross_entropy(input=predict, label=label)
# 计算平均损失
avg_cost = fluid.layers.mean(cost)
# 计算分类准确率
acc = fluid.layers.accuracy(input=predict, label=label)
return predict, [avg_cost, acc]
Optimizer Function 配置¶
在下面的 Adam optimizer,learning_rate 是学习率,它的大小与网络的训练收敛速度有关系。
def optimizer_program():
return fluid.optimizer.Adam(learning_rate=0.001)
数据集 Feeders 配置¶
下一步,我们开始训练过程。paddle.dataset.mnist.train()和paddle.dataset.mnist.test()分别做训练和测试数据集。这两个函数各自返回一个reader——PaddlePaddle中的reader是一个Python函数,每次调用的时候返回一个Python yield generator。
下面shuffle是一个reader decorator,它接受一个reader A,返回另一个reader B。reader B 每次读入buffer_size条训练数据到一个buffer里,然后随机打乱其顺序,并且逐条输出。
batch是一个特殊的decorator,它的输入是一个reader,输出是一个batched reader。在PaddlePaddle里,一个reader每次yield一条训练数据,而一个batched reader每次yield一个minibatch。
# 一个minibatch中有64个数据
BATCH_SIZE = 64
# 每次读取训练集中的500个数据并随机打乱,传入batched reader中,batched reader 每次 yield 64个数据
train_reader = paddle.batch(
paddle.reader.shuffle(
paddle.dataset.mnist.train(), buf_size=500),
batch_size=BATCH_SIZE)
# 读取测试集的数据,每次 yield 64个数据
test_reader = paddle.batch(
paddle.dataset.mnist.test(), batch_size=BATCH_SIZE)
构建训练过程¶
现在,我们需要构建一个训练过程。将使用到前面定义的训练程序 train_program, place 和优化器 optimizer,并包含训练迭代、检查训练期间测试误差以及保存所需要用来预测的模型参数。
Event Handler 配置¶
我们可以在训练期间通过调用一个handler函数来监控训练进度。
我们将在这里演示两个 event_handler 程序。请随意修改 Jupyter Notebook ,看看有什么不同。
event_handler 用来在训练过程中输出训练结果
def event_handler(pass_id, batch_id, cost):
# 打印训练的中间结果,训练轮次,batch数,损失函数
print("Pass %d, Batch %d, Cost %f" % (pass_id,batch_id, cost))
from paddle.utils.plot import Ploter
train_prompt = "Train cost"
test_prompt = "Test cost"
cost_ploter = Ploter(train_prompt, test_prompt)
# 将训练过程绘图表示
def event_handler_plot(ploter_title, step, cost):
cost_ploter.append(ploter_title, step, cost)
cost_ploter.plot()
event_handler_plot 可以用来在训练过程中画图如下:

开始训练¶
可以加入我们设置的 event_handler 和 data reader,然后就可以开始训练模型了。
设置一些运行需要的参数,配置数据描述
feed_order 用于将数据目录映射到 train_program
创建一个反馈训练过程中误差的train_test
定义网络结构:
# 该模型运行在单个CPU上
use_cuda = False # 如想使用GPU,请设置为 True
place = fluid.CUDAPlace(0) if use_cuda else fluid.CPUPlace()
# 调用train_program 获取预测值,损失值,
prediction, [avg_loss, acc] = train_program()
# 输入的原始图像数据,名称为img,大小为28*28*1
# 标签层,名称为label,对应输入图片的类别标签
# 告知网络传入的数据分为两部分,第一部分是img值,第二部分是label值
feeder = fluid.DataFeeder(feed_list=[‘img’, ‘label’], place=place)
# 选择Adam优化器
optimizer = optimizer_program()
optimizer.minimize(avg_loss)
设置训练过程的超参:
PASS_NUM = 5 #训练5轮
epochs = [epoch_id for epoch_id in range(PASS_NUM)]
# 将模型参数存储在名为 save_dirname 的文件中
save_dirname = "recognize_digits.inference.model"
def train_test(train_test_program,
train_test_feed, train_test_reader):
# 将分类准确率存储在acc_set中
acc_set = []
# 将平均损失存储在avg_loss_set中
avg_loss_set = []
# 将测试 reader yield 出的每一个数据传入网络中进行训练
for test_data in train_test_reader():
acc_np, avg_loss_np = exe.run(
program=train_test_program,
feed=train_test_feed.feed(test_data),
fetch_list=[acc, avg_loss])
acc_set.append(float(acc_np))
avg_loss_set.append(float(avg_loss_np))
# 获得测试数据上的准确率和损失值
acc_val_mean = numpy.array(acc_set).mean()
avg_loss_val_mean = numpy.array(avg_loss_set).mean()
# 返回平均损失值,平均准确率
return avg_loss_val_mean, acc_val_mean
创建执行器:
exe = fluid.Executor(place)
exe.run(fluid.default_startup_program())
设置 main_program 和 test_program :
main_program = fluid.default_main_program()
test_program = fluid.default_main_program().clone(for_test=True)
开始训练:
lists = []
step = 0
for epoch_id in epochs:
for step_id, data in enumerate(train_reader()):
metrics = exe.run(main_program,
feed=feeder.feed(data),
fetch_list=[avg_loss, acc])
if step % 100 == 0: #每训练100次 打印一次log
print("Pass %d, Batch %d, Cost %f" % (step, epoch_id, metrics[0]))
event_handler_plot(train_prompt, step, metrics[0])
step += 1
# 测试每个epoch的分类效果
avg_loss_val, acc_val = train_test(train_test_program=test_program,
train_test_reader=test_reader,
train_test_feed=feeder)
print("Test with Epoch %d, avg_cost: %s, acc: %s" %(epoch_id, avg_loss_val, acc_val))
event_handler_plot(test_prompt, step, metrics[0])
lists.append((epoch_id, avg_loss_val, acc_val))
# 保存训练好的模型参数用于预测
if save_dirname is not None:
fluid.io.save_inference_model(save_dirname,
["img"], [prediction], exe,
model_filename=None,
params_filename=None)
# 选择效果最好的pass
best = sorted(lists, key=lambda list: float(list[1]))[0]
print('Best pass is %s, testing Avgcost is %s' % (best[0], best[1]))
print('The classification accuracy is %.2f%%' % (float(best[2]) * 100))
训练过程是完全自动的,event_handler里打印的日志类似如下所示。
Pass表示训练轮次,Batch表示训练全量数据的次数,cost表示当前pass的损失值。
每训练完一个Epoch后,计算一次平均损失和分类准确率。
Pass 0, Batch 0, Cost 0.125650
Pass 100, Batch 0, Cost 0.161387
Pass 200, Batch 0, Cost 0.040036
Pass 300, Batch 0, Cost 0.023391
Pass 400, Batch 0, Cost 0.005856
Pass 500, Batch 0, Cost 0.003315
Pass 600, Batch 0, Cost 0.009977
Pass 700, Batch 0, Cost 0.020959
Pass 800, Batch 0, Cost 0.105560
Pass 900, Batch 0, Cost 0.239809
Test with Epoch 0, avg_cost: 0.053097883707459624, acc: 0.9822850318471338
训练之后,检查模型的预测准确度。用 MNIST 训练的时候,一般 softmax回归模型的分类准确率约为 92.34%,多层感知器为97.66%,卷积神经网络可以达到 99.20%。
应用模型¶
可以使用训练好的模型对手写体数字图片进行分类,下面程序展示了如何使用训练好的模型进行推断。
生成预测输入数据¶
infer_3.png 是数字 3 的一个示例图像。把它变成一个 numpy 数组以匹配数据feed格式。
def load_image(file):
# 读取图片文件,并将它转成灰度图
im = Image.open(file).convert('L')
# 将输入图片调整为 28*28 的高质量图
im = im.resize((28, 28), Image.ANTIALIAS)
# 将图片转换为numpy
im = numpy.array(im).reshape(1, 1, 28, 28).astype(numpy.float32)
# 对数据作归一化处理
im = im / 255.0 * 2.0 - 1.0
return im
cur_dir = os.getcwd()
tensor_img = load_image(cur_dir + '/image/infer_3.png')
Inference 创建及预测¶
通过load_inference_model来设置网络和经过训练的参数。我们可以简单地插入在此之前定义的分类器。
inference_scope = fluid.core.Scope()
with fluid.scope_guard(inference_scope):
# 使用 fluid.io.load_inference_model 获取 inference program desc,
# feed_target_names 用于指定需要传入网络的变量名
# fetch_targets 指定希望从网络中fetch出的变量名
[inference_program, feed_target_names,
fetch_targets] = fluid.io.load_inference_model(
save_dirname, exe, None, None)
# 将feed构建成字典 {feed_target_name: feed_target_data}
# 结果将包含一个与fetch_targets对应的数据列表
results = exe.run(inference_program,
feed={feed_target_names[0]: tensor_img},
fetch_list=fetch_targets)
lab = numpy.argsort(results)
# 打印 infer_3.png 这张图片的预测结果
img=Image.open('image/infer_3.png')
plt.imshow(img)
print("Inference result of image/infer_3.png is: %d" % lab[0][0][-1])
预测结果¶
如果顺利,预测结果输入如下:
Inference result of image/infer_3.png is: 3 , 说明我们的网络成功的识别出了这张图片!
总结¶
本教程的softmax回归、多层感知机和卷积神经网络是最基础的深度学习模型,后续章节中复杂的神经网络都是从它们衍生出来的,因此这几个模型对之后的学习大有裨益。同时,我们也观察到从最简单的softmax回归变换到稍复杂的卷积神经网络的时候,MNIST数据集上的识别准确率有了大幅度的提升,原因是卷积层具有局部连接和共享权重的特性。在之后学习新模型的时候,希望大家也要深入到新模型相比原模型带来效果提升的关键之处。此外,本教程还介绍了PaddlePaddle模型搭建的基本流程,从dataprovider的编写、网络层的构建,到最后的训练和预测。对这个流程熟悉以后,大家就可以用自己的数据,定义自己的网络模型,并完成自己的训练和预测任务了。
参考文献¶
- LeCun, Yann, Léon Bottou, Yoshua Bengio, and Patrick Haffner. "Gradient-based learning applied to document recognition." Proceedings of the IEEE 86, no. 11 (1998): 2278-2324.
- Wejéus, Samuel. "A Neural Network Approach to Arbitrary SymbolRecognition on Modern Smartphones." (2014).
- Decoste, Dennis, and Bernhard Schölkopf. "Training invariant support vector machines." Machine learning 46, no. 1-3 (2002): 161-190.
- Simard, Patrice Y., David Steinkraus, and John C. Platt. "Best Practices for Convolutional Neural Networks Applied to Visual Document Analysis." In ICDAR, vol. 3, pp. 958-962. 2003.
- Salakhutdinov, Ruslan, and Geoffrey E. Hinton. "Learning a Nonlinear Embedding by Preserving Class Neighbourhood Structure." In AISTATS, vol. 11. 2007.
- Cireşan, Dan Claudiu, Ueli Meier, Luca Maria Gambardella, and Jürgen Schmidhuber. "Deep, big, simple neural nets for handwritten digit recognition." Neural computation 22, no. 12 (2010): 3207-3220.
- Deng, Li, Michael L. Seltzer, Dong Yu, Alex Acero, Abdel-rahman Mohamed, and Geoffrey E. Hinton. "Binary coding of speech spectrograms using a deep auto-encoder." In Interspeech, pp. 1692-1695. 2010.
- Kégl, Balázs, and Róbert Busa-Fekete. "Boosting products of base classifiers." In Proceedings of the 26th Annual International Conference on Machine Learning, pp. 497-504. ACM, 2009.
- Rosenblatt, Frank. "The perceptron: A probabilistic model for information storage and organization in the brain." Psychological review 65, no. 6 (1958): 386.
- Bishop, Christopher M. "Pattern recognition." Machine Learning 128 (2006): 1-58.

本教程 由 PaddlePaddle 创作,采用 知识共享 署名-相同方式共享 4.0 国际 许可协议进行许可。